[BOJ 3392]
문제 바로가기 : https://www.acmicpc.net/problem/3392
문제 설명은 위 링크에서 확인해주시길 바랍니다.
solution
review
y축에 평행한 선을 두고 왼쪽부터 오른쪽으로 훑어가면서 면적에 해당되는 부분을 더하면 총 면적을 구할 수 있다.
하지만 30000*30000의 배열을 만들 수는 없기도 하고 일일이 세기에도 시간이 만만찮다.
때문에 면적을 빠르게 계산할 아이디어가 필요하다.
각 직사각형의 세로는 시작선, 끝선이 존재한다. 이 선이 시작하는건지 끝나는건지 표시해둘 필요가 있다.
line을 담는 벡터 lines에 각 세로줄의 정보를 담아주자.
struct line {
int x, lowy, highy;
bool start; //시작선이면 true, 아니면 false
line(int x, int lowy, int highy, bool start) : x(x), lowy(lowy), highy(highy), start(start) {}
bool operator<(const line& l) const { return x < l.x; } //정렬때문에 선언
};
...
vector<line> lines;
for (int i = 0; i < n; i++) {
int x1, y1, x2, y2;
cin >> x1 >> y1 >> x2 >> y2;
lines.push_back({ x1, y1, y2-1, true });
lines.push_back({ x2, y1, y2-1, false });
}
y2에 -1를 해서 담는 이유는 길이를 구하는게 아니라 면적을 구하려고 하기 때문이다.
y=1, y=3을 생각해보자. 이 세로줄에는 1*1 정사각형이 3개가 아니라 2개가 붙는다.
물론 수정해서 이용할 수는 있겠지만.. uplast_modified_at()에 다음과 같이 선언했기 때문에 y2-1이 들어가야 한다.
cnt[]를 설명하지 않아서 혼란스러울 수 있는데 표시한 부분만 보고 끄덕일 수 있으면 된다.
void uplast_modified_at(int node, int ns, int ne, int l, int r, ll val) {
if (r < ns || ne < l) return;
if (l <= ns && ne <= r) cnt[node] += val;
else {
int m = (ns + ne) / 2;
uplast_modified_at(node * 2, ns, m, l, r, val);
uplast_modified_at(node * 2 + 1, m+1, ne, l, r, val);
}
if (cnt[node]) tree[node] = ne - ns + 1; //[ne, ns]에서 사각형의 개수
else
if (ns == ne) tree[node] = 0;
else tree[node] = tree[node * 2] + tree[node * 2 + 1];
}
빨리 계산하려면 세그먼트 트리를 사용해야한다!
세그먼트 트리를 업데이트하는 방식을 설명하기 이전에 어떻게 면적을 구해 나갈 것인지 그림을 통해서 설명하려고 한다.
input을 모두 받고 나서는 왼쪽에 있는 세로선부터 순차적으로 탐색하기 위해 정렬을 해주자.
for (int i = 0; i < n; i++) {
int x1, y1, x2, y2;
cin >> x1 >> y1 >> x2 >> y2;
lines.push_back({ x1, y1, y2-1, true });
lines.push_back({ x2, y1, y2-1, false });
}
//스위핑을 위해 x를 기준으로 오름차순 정렬
sort(lines.begin(), lines.end());
구분을 위해서 빨간색, 초록색 선으로 표시했다. 큰 의미는 없다.
첫번째 사각형의 시작선을 만났을 때 시작선의 구간만큼 +1 해주자.
세그먼트 트리 특성상 첫번째 인덱스가 루트 노드가 되므로 y=10~20에 +1해주면 tree[1]=10이 된다.
앞으로 기본적인 컨셉은 선이 시작선이면 +1을, 끝선이면 -1를 해줄 것이다.
무슨 말인지 모르겠다면 그림을 보면서 따라가면 된다.
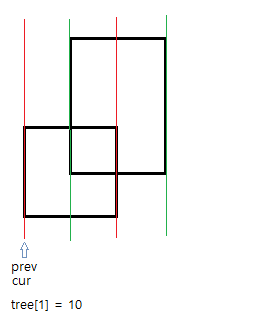
//첫 번째 사각형의 시작하는 변을 만났을 때
line prev = lines[0];
line cur = lines[0];
uplast_modified_at(1, 0, MAX-1, cur.lowy, cur.highy, 1);
다음 선은 두번째 사각형의 시작선이다. 이 선으로 cur을 설정해준다.
prev와 cur이 서로 다른 선을 가리키고 있으므로 넓이를 구할 수 있다!
업데이트해주기 전의 tree[1]은 두 선(prev, cur) 사이에 있는 직사각형의 세로 길이이다.
prev와 cur 사이의 길이 즉, 직사각형의 가로 길이는 dx라고 하자. dx는 5임을 쉽게 알 수 있다.
면적을 구할 수 있으므로 ret에 더해주자. (ret = 50)
그리고 시작선이므로 cur의 구간(15, 30)만큼 +1해주자.
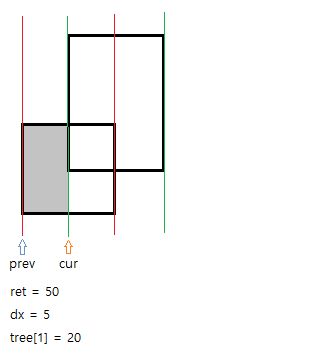
ll ret = 0;
for (int i = 1; i < 2 * n; i++) {
cur = lines[i];
int dx = cur.x - prev.x;
ret += dx * tree[1];
if(cur.start) uplast_modified_at(1, 0, MAX-1, cur.lowy, cur.highy, 1); //시작선
else uplast_modified_at(1, 0, MAX-1, cur.lowy, cur.highy, -1); //끝선
prev = cur;
}
세번째 선은 첫번째 사각형의 끝선이다. 이 선이 cur이 되겠다.
현재 tree[1]가 20이고 dx가 5이므로 ret에 100을 더해주자. (ret = 150)
그리고 cur은 끝선이므로 구간(10, 20)만큼 -1을 해줘야 한다.
+1, -1을 해준다는건 tree[1] 즉 직사각형 면적의 세로 길이에 영향을 주는걸 말한다.
하지만 구간만큼 +1, -1을 해줘도 길이가 그만큼 늘어나고 줄어들지 않는다. 그래서도 안된다.
그러나 더해주거나 뺄 때 길이에 영향을 주는건 분명하다. uplast_modified_at()를 보면 왜 인지 알 수 있다.
이 부분은 면적을 모두 구하고 나서 마지막에 설명하겠다.
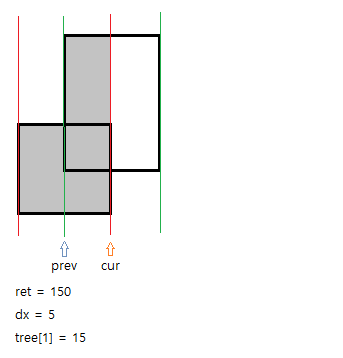
마지막인 네번째 선이 도달했다. 두번째 사각형의 끝선이다.
현재 tree[1]가 15, dx가 5이므로 ret에 75를 더한다. (ret = 225)
더 이상의 업데이트는 의미가 없으므로 tree[1]이 몇인지는 표시하지 않았다.
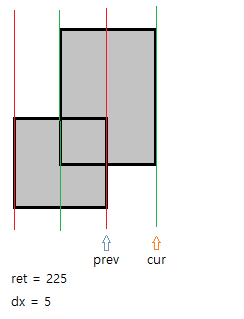
그럼 방금 언급했던 +1, -1은 어떤식으로 작동하길래 필요한 만큼만 늘어나거나 줄어들까?
구간별 업데이트라고 하면 보통 lazy propagation을 떠올리기 쉽다. 실제로 그렇게 구현한 사람도 봤다.
하지만 이 문제는 구간을 업데이트 하지만 lazy propagation을 사용하지 않고도 답을 구할 수 있다.
정확히는 비슷한 아이디어를 사용한다고 보면 될 것 같다. tree[] 이외에도 cnt[]를 선언해 이용한다.
최대, 최솟값을 계산하는 세그먼트 트리처럼 구간 내에 [ns, ne]가 들어오면 재귀호출을 중단한다.
그리고 tree[node]가 아닌 cnt[node]에 일단 val을 더한다. (lazy propagation과 비슷하다고 한 부분)
그렇게 반영한 cnt[node]가 0이 아니면 tree[node]를 현재 구간에 있는 면적(ne-ns+1)만큼 저장한다.
만약 cnt[node]가 0인데 리프노드라면 0을, 아니라면 자식 노드의 합으로 저장한다.
cnt[node]가 0이 아니라는건(정확히는 cnt[node]>0) 현재 구간[ns, ne]이 유효하다는걸 의미한다. 유효하면 1을 유지한다.
아까 세로선들마다 업데이트 했던걸 그림 하나로 나타내면 다음과 같다.
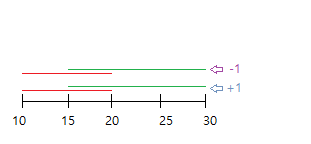
세번째 선때문에 [10, 20]이 -1돼도 첫번째 선만큼만 상쇄될 뿐 두번째 선을 때문에 [15, 30]이 유효하다!
개인적으로는 상당히 어렵게 느껴졌던 문제였다.
스위핑에 대한 이해가 떨어지기도 했고 다른 알고리즘과 섞어서 응용해 풀기엔 아직 많이 부족한 것 같다.
각 유형을 숙지하고 응용할 수 있는 단계까지 나아갈 수 있도록 많은 경험을 해봐야겠다.

댓글남기기