[BOJ 2150]

문제 바로가기 : https://www.acmicpc.net/problem/2150
문제 설명은 위 링크에서 확인해주시길 바랍니다.

Solution

Strongly Connected Component

crocus님의 글을 참고 했습니다. 감사합니다.

노드 u, v가 있을 때 u에서 v로, v에서 u로 이동할 수 있을 때 강한 결합 요소(Strongly Connected Component)라 한다.
방향이 없는 그래프는 무조건 SCC가 된다. 따라서 방향 그래프인 경우 의미가 있다고 할 수 있겠다.
SCC를 찾는 알고리즘은 코사라주, 타잔 알고리즘이 있다. 전자는 구현이 쉽고 후자는 적용이 쉽다.
나같은 경우 타잔 알고리즘으로 구현했다. 자세한 설명은 위 글을 참고.

review

먼저 이 알고리즘은 dfs()를 통해 연결된 노드로 이동하면서 부모 노드를 만났을 때 더 이상 dfs()를 멈추고 돌아간다.
그리고 dfs(부모)로 돌아왔을 때 아직 가지 못한 연결된 노드로 계속 진행한다.

BOJ 2150에 있는 TC를 그려보면 다음과 같다.


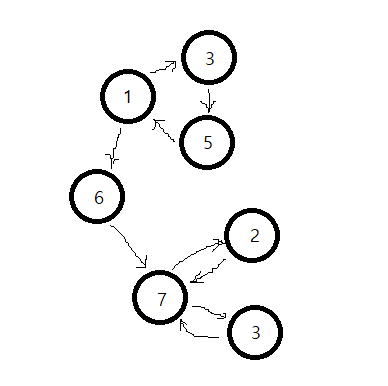
dfs()는 1번부터 시작하도록 돼있으며 이미 수행된 노드(chk[cur] != 0)는 다시 수행하지 않도록 한다.
for문에 들어가게 되면 이웃된 노드(next)를 탐색하는데 dfs()가 수행되지 않았다면 수행하고(dfs(next)), 수행된 상태라면 chk[next]만 이용한다. 어떻게 진행되는지 간략하게 써보자.
for문에 들어가기 전 단계를 잘라서 정보를 적었다.

dfs(1)
: chk[1] = 1
: parent = 1

stack : 1

그리고 for문에서 1과 이웃된 4를 탐색하고 그 다음인 5까지 진행한다.

dfs(1)
: chk[1] = 1
: parent = 1
  dfs(4)
  : chk[4] = 2
  : parent = 2
    dfs(5)
    : chk[5] = 3
    : parent = 3

stack : 1 4 5

dfs(5) 안에 for문에서는 next가 이제 1밖에 없다. 근데 1은 dfs()가 이미 수행이 돼버렸다.
이를 chk[1] != 0 에서 알려주고 있으며, else if문으로 넘어가 chk[1]을 이용한다.
조건 안에 있는 fin[next]는 next가 SCC에 들어갔는지를 말한다. 1은 아직 들어가지 않았다.
그럼 dfs(5)는 parent가 1로 업데이트 된다. 사이클이 발생했음을 알게 되는 순간이다!

그리고 dfs(5)는 1을 반환하면서 dfs(4)의 parent도 1로 만들어준다.
이후 dfs(1)로 돌아오고 dfs(4)가 1을 반환했지만 parent가 이미 1이므로 변함이 없으며 6을 탐색한다.
dfs(6)에서는 연결된 7번으로 들어가 다시 dfs(7)을 수행한다.

dfs(1)
: chk[1] = 1
: parent = 1
  dfs(4) *종료
  : chk[4] = 2
  : parent = 1 <-
  : return 1
    dfs(5) *종료
    : chk[5] = 3
    : parent = 1 <-
    : return 1 <-
  dfs(6)
  : chk[6] = 4
  : parent = 6
    dfs(7)
    : chk[7] = 5
    : parent = 7

stack : 1 4 5 6 7

이후에도 전과 방법이 같으므로 어떻게 돌아가는지 감이 잡힐 것이다.
마지막 노드까지 탐색하면 다음과 같다. 이해가 안간다면 직접 천천히 그려서 점검해보자.

dfs(1)
: chk[1] = 1
: parent = 1
  dfs(4) *종료
  : chk[4] = 2
  : parent = 1 <-
  : return 1
    dfs(5) *종료
    : chk[5] = 3
    : parent = 1 <-
    : return 1 <-
  dfs(6)
  : chk[6] = 4
  : parent = 4
    dfs(7)
    : chk[7] = 5
    : parent = 5
      dfs(3) *종료
      : chk[3] = 6
      : parent = 5 <-
      : return 5 <-
    dfs(2) *종료
    : chk[2] = 7
    : parent = 5 <-
    : return 5 <-

stack : 1 4 5 6 7 3 2

그럼 7, 6, 1 순서대로 dfs가 종료되는데 7, 6, 1이 부모 노드이므로 스택에서 자르게 되는 기준이 된다.

ans : 1 4 5 / 6 / 7 3 2

백준에서 단계별로 풀어보기 문제집을 입문으로 시작한지 3개월 정도 됐다!
예전에는 상상도 못할 난이도의 문제가 속속 등장하기 시작했다. 2~3일마다 새로운 알고리즘을 익히는거 같다..
어떻게 돌아가는지 파악하고 소화하는데까지 아직도 시간이 많이 걸린다. ㅠㅠ
시간을 들여서 풀 수는 있겠는데 타임 어택으로 풀라고 하면 한없이 부족할 때도 있고.. 더 달려봐야겠다.